power levels & impedance

home
back to articles
back to technical explanations

published: Dec-11-2013, last update: Nov-15-2025

Power levels, efficiency, impedance, voltages, current, sound pressure…
Can you make heads nor tails ?

What is the relation between resistance and impedance and how will this affect the sound ?
In most forums there is lots of speculation, information and above all mis-information about output resistances of amplifiers, impedance of headphones, cables and how they relate.
The biggest problem is there are facts and fiction mixed and spread over large quantities of posts. This makes it very difficult to discriminate between facts and nonsense.
The article resistance, impedance and other issues  covers a lot of often asked questions and puts them in an (I hope for most) understandable context.
It will let you catch up on some basics on resistance, impedance, damping factor, output resistance, cables.

Ever wondered HOW much power you actually need for your headphone(s) ?
Download/view the pdf from the link below:
headphone power table 2025
How much Voltage and/or Current and power is needed and.. how loud can your headphone actually play ?
The table has over 800 ‘familiar’ headphones in it (only on-ear and over-ear)

How loud you play your music will largely depend on our preference in music, recording quality (piercing treble,  lots of bass or a nice clean recording) and the dynamic range of that recording.To get an idea (it is not the final truth) about which album has how much dynamic range you can look for artists and albums HERE.
A high or low dynamic range doesn’t mean an album or song sounds better or worse. It only says something about how many dB’s peaks and average levels are apart. For instance an album with DR8 has peaks that are 8dB louder than the average levels.
The average level determines how loud we perceive the music and the peaks are not necessarily heard as peaks.
An album with a DR16 thus has 16dB higher peaks than the average levels and is more dynamic.

How loud do we actually play our music ?

This isn’t a really easy question to answer as it depends on how one prefers to listen and to what music.
More accurately how well a recording was made and what the Dynamic Range of the recording is.
Peaks can be much higher than the average levels and it is the average levels that more or less determine how loud one perceives the music.
A popular music recording with a DR6 or so you can’t turn up as far as a DR16 recording because the average levels are already 10dB louder. Out of interest in how loud I actually hear I decided to listen to a recording while measuring the output level of the amplifier.
The reason why you can’t really use a dB meter is because it averages, even in peak mode it doesn’t register very short attacks that well. At least the cheaper SPL meters I have. So I used a song from Paul Simon from the original CD.
The DR database had the following info:
Analyzed: Paul Simon / There Goes Rhymin’ Simon / 1987
DR13 -2.55 dB -19.57 dB 3:31 03-Take Me To The Mardi Gras
A DR13 recording is actually quite decent and this recording does sound very dynamic and free of distortion.

Below a table with loudness descriptions used on this website and the expected average and peak levels as well as recommended maximum exposure limits.

Test conditions:
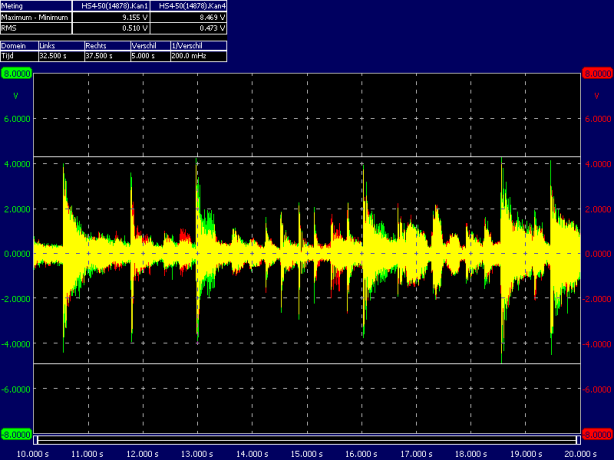
FiiO X3, line-out > Kameleon + HD650 module ↦ HD650 > my ears.
the headphone signal was splitted to a HS4/50 oscilloscope in peak detect mode.
During a time frame of 10 seconds (in various parts of the song) the signal was logged and peaks were measured and displayed.
The RMS value of the 10 second section is shown as well as the peak-to-peak voltage.
As we want the RMS value of the peaks that occur we need to convert the peak-peak voltage to RMS.
To do this we need to find the peak value by halving the peak-peak value and take the √2.
As this factor will be the same for all calculations it is easier to multiply the peak-peak value with 0.354
Because we now have the RMS voltage and the impedance (320 Ω) we can calculate the power using ((U_RMS)² / 320)x1,000) = mW. The HD650 has an efficiency of 98dB @ 1mW (measured by Innerfidelity).
As the measured power and the amount of dB is known at 1mW we can calculate the SPL.

Below the scope data from a (random part in the song) chosen 10 second excerpt from the recording.

note: For young people (< 25.y.o.) the perceived loudness may be about several dB lower than shown in the tests below.
The lower hearing limits climb upwards as one ages.
Young folks thus perceive sounds at the given power levels about 10dB louder (twice as loud) as older folks.

note2: dB SPL is not the same as dBA (or Phon). This article is about dB SPL and not dBA !

---

The part of the recording shown below was playing very softly, think soft level when listening in the evening. The level where you can easily listen for a whole evening while having the urge to turn up the volume a bit.
This is slightly below the level I usually listen at. My ‘normal’ listening level is around 75dB average.

This resulted in the following (rounded off) numbers:

RMS levels = 23mV = 0.0017mW = 70dB (average)
Peak levels = 245mV_PP = 87mV_RMS = 0.023mW = 82dB
calculated DR = 11.5dB for that 10 sec of the song.

---

The plot below shows part of the recording was playing at a very comfortable level that is a fair bit louder than the soft level. You can listen a whole evening to this level. This is slightly above the level I usually listen at.
On lower DR recordings you like to turn it down a slight nudge, higher DR recordings you may feel the urge to turn it up a tad.

This resulted in the following (rounded off) numbers:

RMS levels = 75mV = 0.018mW = 80dB (average)
Peak levels = 830mV_PP = 293mV_RMS = 0.26mW = 92dB
calculated DR = 11.8dB for that 10 sec of the song.

---

The  part of the recording below was playing at a comfortably loud level which is easy to listen to for 1 or 2 songs before getting the urge to turn it down to more comfortable levels.
When I really like a song I might turn up the volume to this level but turn it down again after 1 or 2 songs.

This resulted in the following (rounded off) numbers:

RMS levels = 236mV = 0.174 mW = 90dB (average)
Peak levels = 2.63V_PP = 930mV_RMS = 2.7mW = 102dB
calculated DR = 11.9dB for that 10 sec part of the song

---

This part of the recording below was playing loud. It is the type of level where you turn up the volume because you either like the song very much or want to listen ‘deep’ in the recording to evaluate.
Not a level you would gladly endure for the whole song.

This resulted in the following (rounded off) numbers:

RMS levels = 510mV = 0.81mW = 97dB (average)
Peak levels = 9.16V_PP = 3.24V_RMS = 33mW = 113dB
calculated DR = 16dB for that 10 sec part of the song
(this was the intro of the song by the way)

---

Here the music is playing at quite uncomfortably loud levels. One may use these levels for listening ‘in the recording’ for analytic purposes to check for distortions or find noise levels in the recording.
These levels are certainly NOT used for pleasantly enjoying music and one, for sure, cannot maintain to listen to these levels for the whole song.
It should be noted though that this is a DR13 recording and this particular part was ‘just’ 12dB DR.

When listening to DR20 recordings the average levels will be quite loud but the peak levels will reach about the same 117dB peak levels.
The amplifier started clipping the highest peaks already which added a sharp ‘edge’ at certain peaks.
I would not call those peaks anywhere near ‘pain levels’ though but ‘very loud’ none the less.

This resulted in the following (rounded off) numbers:
RMS levels = 1.35V = 5.6mW = 105dB (average)
Peak levels = 15V_PP = 5.3V_RMS = 88mW = 117dB peak
calculated DR = 11.9dB for that 10 sec part of the song.

I certainly do not recommend listening to these levels for longer than 1 minute or so.

---

This data shows that to drive the HD650’s to uncomfortable loud levels while still not nearing any clipping levels and having a few dB extra headroom you will need an amplifier that can supply at least 10V_RMS which means the amplifier must be able to supply 300mW into 300Ω headphones. When that amplifier is low resistance and can provide the same voltage in 32Ω headphones it must be specified for 3W into 32Ω.
To drive the HD650 to comfortably loud levels you only need around 1.7V_{RMS =} 10mW into 300Ω though.
A player that is specified to reach 100mW in 32Ω thus will be able to do that job.

Of course the voltage levels for driving an equally efficient (dB’s per mW) headphone will be substantially lower.
Currents will be the same magnitude higher.
The numbers above are thus only applicable to 250Ω to 300Ω headphones.
For the very few 600Ω headphones around you can multiply the needed VOLTAGES by a factor 2.

How much power do we need ?

Most headphones do not need a lot of power (check the headphone power table 2025) play sufficiently loud.
Only very few inefficient ones do and these don’t even need that much power as most people think.

It doesn’t hurt to have a surplus of power available unless you are using headphones that cannot handle a lot of power.
In this case you run the risk of burning out the voice coils by accident (when not on the head) but will never run into clipping.
Having a surplus (in power) of a factor 10 won’t hurt but  may never or hardly ever be used.

Having too little power (voltage actually) won’t damage any voice-coils but higher impedance headphones won’t reach decent SPL levels.
Too little power results in not very dynamic and ‘meager’ sound in general.
Driving a high impedance headphone like HD800 or HD600 from a phone won’t give a satisfying sound simply because the output voltage ‘clips’ before a decent listening level is reached. IF you only like to play music very softly there is no problem.
For this reason many people draw the conclusion they need more power .
They DO of course, as power is related to voltage but it is not that one needs more POWER.
P (watt) = U²(voltage) x impedance (Ohm), but what high impedance headphones really need is more voltage.

Because of these facts the myth is born ‘more power = better sound’.
It has some truth in it though.

Having an amp that can deliver 10W, if your headphone can only handle 0.2W, won’t sound better than when playing it from an amp that can deliver just 1W or maybe even ‘merely’ 0.1W (100mW).
Of course, you also need to include the psychological factor of having the ‘knowledge’ the amp will never reach its limits and you have ‘power’ in your hands.

For instance, an amp may deliver 1W into 16Ω but the same amp will only deliver 0.025W into a 600Ω headphone (assuming the current limit is not reached and output resistance is low)
Someone that THINKS he just bought a powerful amp (it is 1W for heavens sake!) will not be able to drive a 600Ω headphone very loud.
So one may think.. I need a much more powerful amp.
You don’t, you just need an amplifier with a higher output voltage, not necessarily meaning a more powerful amp.

It works the other way around too.
An amplifier that can deliver 1W into 600Ω only needs to deliver 40mA (60mA pk) to achieve that power.
Let’s assume the amp is current limited to 60mA.
When you connect a 20Ω headphone to that same amp it will only deliver 0.032W into it.

Power specs are thus MEANINGLESS unless they are accompanied by the headphone impedances that it must drive.
This too adds to the needs more ‘power’ or ‘headphone X or Y’ is hard to drive myths on the web.

This is just the technical part though, as many will say that doesn’t account for everything that is perceived.

Now, let’s assume we do not want to play very loud and have no need to play any louder than say 105dB peak levels.
This means for high DR recordings average levels of 90dB will be present

If you want to be able to drive all commercial headphones to 105dB (peak) but with NO headroom to spare, you will need an amplifier that can reach certain minimal voltage, current and thus power levels, remember P (Watt) = U (Volts) x I (Amps) .
We are going to differentiate between sensitive and ‘hard to drive’ headphones and 2 tranches in between those values.

Some examples of known headphones from the mentioned headphone power table 2025

very sensitive low impedance headphone: (ATH-ES10 for instance) needs 0.25mW, 0.1V,  2.5mA to achieve 105dB SPL.
very sensitive high impedance headphone:  (GMP 435Sfor instance) needs 0.25mW, 0.25V,  1mA  to achieve 105dB SPL.

average sensitive low impedance headphone: (Beyer T70P) needs 1.26mW, 0.2V,  6mA
average sensitive high impedance headphone: (Beyer T70) needs 1.26mW, 0.6V,  2mA

average less sensitive low impedance headphone: (K550) needs 6mW, 0.5V, 13mA 
average less sensitive high impedance headphone: (DT770/600) needs 8mW,  2V,  4mA 

difficult ones like:
K172 needs 160mW, 3V, 50mA
K240 sextet (600 Ohm) needs 40mW, 4.9V, 8mA
one of the most demanding headphones around, the HE6 needs 630mW,  5.2V, 120mA
and the hardest exotic one K1000 needs 1.3W, 13V, 91mA

For 90dB average (105dB peak) on high DR recordings we need.
most sensitive headphones around: 0.2mW,  0.1V,  2mA  
average sensitive headphones: 1.6mW,  0.3V,  5.5mA
somewhat less sensitive headphones: 29mW, 1.7V,  17mA 
difficult to drive ones: 270mW, 4.5V, 60mA 
the VERY few insensitive ones: 1.5W, 13.5V, 110mA

For driving most common headphones to 105dB peak levels one ONLY needs 3V and 20mA  = 0.06W (60mW) which most simple and battery fed C’Moy amps should be able to deliver effortlessly.

When driving ONLY sensitive ones:
0.3V x 3mA = 0.1mW is needed that is 0.0001W which can be supplied by the smallest portable players/mobile phones.

Lets assume you want a beast of an amp or occasionally play at loud, and not distorted levels, and want to reach those peak levels of 120dB things change radically as currents and voltage levels increase by 15dB which means a factor 5.5 and for power even by a factor 30.

So IF you want to listen to an HE6  loud on high DR music:
HE-6:  15V x 360mA  = 5.5W

For average headphones  the amplifier needs to be able to deliver 6V and 50mA

For specific difficult ones like K172 = 1.6W, 10V, 165mA  or  K240 sextet (600 Ohm) 0.4W, 16V, 26mA

Lets assume you want a beast of an amp that has no problem playing peaks of 120dB things change radically as currents and voltage levels increase by a factor 5.5 and power by a factor 30

So IF you want to listen to an HE6 REALLY loud on high DR music:
HE-6:  29V x 0.6A  = 17W (voice coil would burn out !)

most sensitive headphones around: 6mW,  0.6V,  10mA 
average sensitive headphones: 50mW,  1.7V,  30mA 
somewhat less sensitive headphones: 1W, 9.5V,  100mA  (damage may occur to some)
difficult to drive ones: 8W, 24V, 0.33A   (some will never reach it and burn out !)
the VERY few insensitive ones: 45W, 75V, 0.6A  (those will never reach it and burn out !)

So IF you like to play high DR recordings really loud for very short periods you need high powered amps.
If you like to play high DR recordings comfortably loud, but with no headroom to spare you don’t need nearly that much.

home
back to articles
back to technical explanations