sensitivity, efficiency & more

home
back to articles
back to technical explanations

published: Jul-02-2025, updated Nov-18-2025

Not all headphones play equally loud on the same volume control setting when connected to the same device.
There is a number that gives information about how loud headphone will play when a voltage is applied to it. This is the sensitivity or efficiency number that is often found in the specifications.

A combination of impedance and sensitivity yields another metric called efficiency.
sensitivity is expressed in dB/V
efficiency is expressed in dB/mW.
So sensitivity and efficiency are not the same thing but are often mixed up.

How loud a headphone will play when 1V is applied or how loud a headphone will play when 1mW (milli-Watt) of power is applied will tell how much Sound Pressure Level (SPL) will be produced.
This number is expressed in dB SPL (deciBell).
0dB does not mean there is no sound pressure at all but is 0.00002 Pascal which is close to the human lower hearing limit under ideal circumstances.
Here is a table that has all the needed info for over 1,000 on- and over-ear headphones updated July 2025: headphone power table 2025

Below some ‘listening level descriptions’ with average (not dBA but dB SPL) levels and peak levels that may occur.
Ensure that the used amplifier has enough power to make the headphone reach at least the listed peak levels but having 6dB ‘extra headroom’ is always good to have.

A sensitivity number of 105dB/V means the headphone (at a specific frequency or frequency band) produces 105dB(SPL) when 1V is applied to it.

An efficiency number of 95dB/mW means the headphone (at a specific frequency or frequency band) produces 95dB(SPL) when 1mW of power is applied to it.

The least sensitive headphones are 85dB/V where the most sensitive headphones are 125dB/V.
When we also include IEM’s the most sensitive ones are around 140dB/V and have an impedance of just a few Ω.

there is more to it … 

Alas …. it isn’t just as simple as looking at a number in a brochure, datasheet or website.
There are several reasons for that. The numbers quoted by manufacturers are, more often than not, incorrect.

Mostly,  just a ‘number’ is given without specifying it is dB/V or dB/mW, nor the frequency it is measured at.
dB/mW and dB/V are sometimes even mixed up, even in spec sheets or not mentioned at all, just a number.

Unfortunately we cannot trust the numbers published by headphone manufacturers.
The reason for that usually lie in the method or the frequency used to determine the sensitivity.
An important factor is at which frequency or frequency band this number is measured.
Rarely it is specified at which frequency, or frequency band the SPL is measured. Is it done using a ‘warble’ tone (a frequency that shifts a bit around the intended frequency) or a fixed frequency sine-wave or even a narrow ‘noise band’ or wide noise band. This alone can lead to different numbers for the same headphone.
On the plot below (which is referenced to 90dBSPL at 1kHz) it is clear that depending on the frequency (band) where sensitivity is measured that it does not really matter if it is measured at 400Hz or 1kHz (the most common used frequencies) or even an average or peak value of a 300Hz-3kHz noise band signal.400Hz = 91dB, 1kHz = 90dB, average of the noise band is also around 90dB
The frequency (band) where this headphone is measured will give very similar numbers.

Below another headphone that, when measured under similar conditions would give substantially different numbers depending on the used frequency, frequency band and if it would be peak value or average value of that noise band. (which is referenced to 90dBSPL at 400Hz) 400Hz = 90dB, 1kHz = 83dB, average of the noise band is around 82dB where the peak value would be 91dB.

It thus matters a lot at which frequency the sensitivity is measured. The difference between measuring at 400Hz and 1kHz for this particular headphone is a substantial 7dB.
Unfortunately the frequency the measurement is performed at is rarely mentioned/specified.

Below we have 2 headphones with a different tonal balance. When both were measured at 1kHz to be 90dB/mW one would get plots like the ones below.
The headphone above has ‘natural’ mids but has a sharp sound and lacks ‘body’ and bass.
When compared to the headphone below (which measures 90dB at 1kHz too) the one below will be perceived quite differently.
bass and lower mids are perceived twice as loud (+10dB is perceived as roughly 2x as loud) and sounds overly bassy lacking clarity/brightness.
So despite these headphones having the same measured efficiency/sensitivity at 1kHz they will not sound equally loud.

Measuring the sensitivity (or efficiency) at a specific fixed frequency is not the best way to determine the sensitivity/efficiency.

As most of the perceived loudness of music is in the middle frequency range (between roughly 200Hz and 5kHz) it is best to determine the efficiency/sensitivity by comparing the average of the measured headphone with a known reference of a headphone in that part of the frequency range of the (known sensitivity) headphone like the one below.

This way one can get a fairly accurate ‘sensitivity’ rating for that headphone. When the tonal balance in that part of the frequency range is not deviating too much the headphones will sound equally loud.
When there is more or less bass or treble then only the bass and treble will sound elevated or lacking but it will be perceived as equally loud.
This is how the sensitivity ratings (and by extension the calculated efficiency ratings) are determined on this website.

In order to compare how loud headphones play at the same volume setting (assuming the output impedance is max. a few Ω) one must use the sensitivity rating (dB/V)

What does the headphone impedance have to do with this ?

For the sensitivity rating (dB/V) the impedance does not play a role.
For the efficiency rating (dB/mW) the impedance plays a substantial role.

Two headphones with a different impedance and both being 100dB/V will play equally loud at the same volume control setting/output voltage while the applied power will differ.
1V in 16Ω = 62.5mW
1V in 600Ω = 1.6mW
Note these headphones will thus play equally loud = 100dB(SPL) on the same volume control level.
But the low impedance headphone draws 40x more power and thus is much less efficient.
While the sensitivity of the 16Ω headphone is 100dB/V the efficiency is 82dB/mW 
While the sensitivity of the 600Ω headphone is 100dB/V the efficiency is 97.8dB/mW

The efficiency numbers for headphones with a different impedance are not directly comparable

This is not so easy for efficiency numbers because this assumes 1mW of applied power.
To create 1mW of power in a 16Ω load we need 0.126V. To create 1mW of power in a 600Ω load we need 0.775V.
This means that when both the 16Ω and 600Ω headphone are rated at 95dB/mW they will not sound equally loud when driven from an amplifier that produces 1V.
When 1V is applied the 16Ω headphone will produce 113dB(SPL) while the 600Ω will produce 97dB(SPL)

This means that when looking at ‘efficiency’ and ‘sensitivity’ numbers in a spec sheet we must look at the letters behind the number, whether it says dBV or dBmW.
When one sees dB/mW and wants to compare 2 headphones with different impedance then one has to convert dB/mW to dB/V first.
Luckily there are several handy on-line converters for this.

• RAA calculator
• headphone palace calculator  (they have more converters)
• Benchmark calculator (they also have a lot more converters)
• spuriae calculator

Or just do a search for: “dBmW to dBV calculator headphones“

One fills in the dB/mW number and impedance and selects dB/mW SPL and then the ‘calculate’ button and there you get the dB/V number.

The impedance of a headphone also matters in another way other than for the efficiency number.
More on this aspect is found HERE.

How loud a headphone can play also depends on the power rating.

All headphones are limited in how much electrical power they can handle.
This too is a rating that is not always given or is unclear.
Power ratings of headphones can vary between 30mW (0.03W) and a few Watt.
Usually the headphones that are very sensitive also have a low power rating.

power rating

There is a substantial difference between a continuous power rating and a peak- or music-power rating.
Headphone amplifiers usually specify either a max power output rating (at a certain impedance) and these numbers are always continuous power which is usually also the peak-power.

Headphones are intended to be used with music. Music is dynamic and is not a continuous signal (like a test signal).

Below an oscilloscope shot from a piece of (dynamic) music.

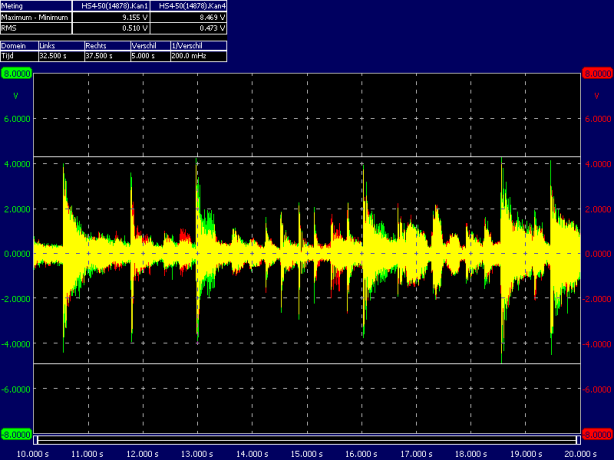The power that is applied thus consists of short peaks and the rest of the time the applied power is considerably less. This means that the average power is much lower than the peak power.
It is the average power level that should not exceed that of the voice-coil of the driver. When that happens the voice-coil over-heats and either deforms or simply goes open circuit. That driver is ‘blown’.

The bad news is that most manufacturers either do not list the max. power rating or fail to mention whether this is continuous-, music- or peak-power and how long that power can be applied without any damage to the driver.
I have created a headphone power table 2025 with most (but certainly not all) over- and on-ear headphones that I managed to find (or estimate) the power rating from.
Here one can find how loud the listed headphones can play, their power rating, impedance, sensitivity and efficiency. It is unclear if the ratings are ‘continuous’ or ‘peak’ so best to assume these are peak values.

How loud a headphone can play thus depends on the sensitivity (dB/V) and how much voltage the connected device can supply to that headphone where one should not exceed the max. power rating of the headphone.

amplifier power or rather … output voltage

All devices with a headphone (or speaker) output have internal amplifier circuits (2 for stereo and 4 for balanced stereo) that are designed to drive the connected devices be them headphones or speakers.

It is important to know that an amplifier is a voltage source and not a power source.
It is the combination of output voltage and current that determines how much power the amp can deliver in a certain impedance headphone.

Amplifiers are voltage sources. This means that when a certain output voltage is present this does not change when a different impedance is connected to it.
An amplifier that has 1V on its output will supply that 1V regardless if the load impedance is 16Ω or 600Ω (assuming the amplifier can deliver the required current in the lowest impedance).

All amplifier circuits have limits though.

• frequency range limits (not relevant here)
• max. output voltage limits
• max. output current limits
• output impedance

Every amplifier has internal voltage rails. It is the internal voltage rail (which does not have to be the same as supply voltage) and the amplifier circuit itself that determines the maximum output voltage swing it can supply before the output clips.

Every amplifier also has current limits. When the current reaches its limit the output voltage won’t be able to go any higher. Current limited clipping usually is a little different in behavior than voltage rail clipping.
The ‘effect’ is similar though with the difference that when the voltage clips the maximum output voltage is reached where as the current clips the maximum output voltage is lower than when voltage clipping occurs. 

Low impedance headphones usually will cause current limited clipping where higher impedance loads will lead to a higher clipping voltage, determined by the internal voltage rails.
An amplifier may well reach 8V in high impedance headphones but only 3V (for instance) in a low impedance headphone.

When someone owns more than one headphone or expects to buy other ones in the future it may pay to buy an amplifier that can supply enough voltage and current (so power in various impedances) so that all headphones can be properly driven to loud levels without ever hitting clipping levels. 
This could, however, lead to owning an amplifier that is capable of delivering way too much power in certain high-efficiency head-/ear-phones (the 20mW / 30mW rated ones) and accidentally blow the drivers in an unforeseen situation.

Also… one should realize that most headphones have a sensitivity number between 95dB/V and 115dB/V which basically means that 1V will be enough to make them play loud enough for listening to music at ‘comfortable loud’ listening levels.

The crazy power levels (> 0.5W) are really only needed when one wants to play really, really LOUD without an amp clipping and even then this is really only needed for a few insensitive (inefficient) headphones.
It is good to realize that when one wants to play music about twice as loud one needs 10dB more power.
This also means 10x more power. When one wants go twice as loud again you need 10dB more power yet again thus requiring 100x more power (20dB more) in total.
Below a table that shows what power increase is needed for a certain level increase.
1dB is just noticeable, 3dB is a doubling of power and 6dB a doubling of voltage. Both of these are easily audible. Every 10dB increase is (close to) a perceived doubling of loudness (sound intensity).When realizing that most headphones are in the 90dB/mW and 100dB/mW efficiency range is easy to see that to reach 110dB (peaks), which is already loud, only 10dB to 20dB is needed so 10mW to 100mW is usually more than enough to play really loud.
One only needs a LOT of power for the rare inefficient headphones (80dB/mW range) or when one has a fairly inefficient headphone and wants to play uncomfortable loud (120dB peaks).

amplifier output resistance

All amplifier circuits also have an output resistance (impedance actually).
A resistance implies that the current and voltage are directly related in amplitude and phase for all frequencies.
An impedance is more complex ‘resistance’ and the voltage and current may not be in phase and may differ per frequency as well.

The same is true for the loads (i.e. headphones/speakers).
There are not many headphones (nor speakers) that behave like a ‘pure resistance’ in the audible frequency range. Most headphones/speakers have a varying impedance.
It is this varying impedance (especially low impedance) in combination with a higher than several Ω output resistance amplifiers that causes tonal changes in headphones.
More info about this aspect can be found HERE.

Most portable devices have a very low output resistance/impedance as do most of the current headphone amps and DAC/amp combinations. 
However, there are a few amplifiers that have a higher output resistance. The problem is that most spec. sheets do not mention the output resistance and often only ‘report’ for which headphone impedance range that device is suited.
External USB sound cards with headphone out also can have a higher output resistance up to 50Ω or so.
The highest output resistance is found in some (OTL) tube amplifiers and above all on integrated amps, receivers and even some AV-Receivers. The ‘headphone out’ of such devices, more often than not, consists of the speaker out signal simply attenuated with some resistors to pad the voltage down.
Output resistance of such outputs can be anything between 50Ω to 600Ω and are bound to change tonality of quite a few headphones.

What power do you need to drive a specific headphone

It is the combination of the output capabilities of an amplifier and load characteristics of the headphone/speaker that determines how loud that combination can play before it hits 1 or more of the limits.

For headphones there is only the max. available output voltage/current/power and the headphone properties.

To determine how loud a headphone can play or to find out how loud a specific headphone can play from a known device all we need to know is the sensitivity (dB/V), The maximum peak SPL (in music) we occasionally want to reach and the headphone impedance.
The impedance and sensitivity numbers can be found here and also on some other sites as well as spec sheets and a lot of them are found here: headphone power table 2025

The first thing to determine is what the max. peak SPL is that, maybe just occasionally, needs to be reached.
There is a lot of misinformation about how much power is needed and often see the familiar ‘average noise exposure limit’ drawings/plots/info.
Just know these are NOT applicable to (dynamic music). Note: I do not recommend to listen to loud music, certainly not for longer time periods.
That said, and taking possible EQ in the bass that may be needed one needs to realize that in order to make a source not reach clipping levels one needs enough ‘headroom’ to correctly reproduce peaks in music. So … don’t be alarmed to see the following recommendations for peak levels. Remember… average levels can easily be 6dB to 20dB below those peaks depending on the recording (DR number).

To ensure you won’t reach clipping levels and even use EQ in the bass one must be able to make a headphone reach 120dB SPL.
This does not mean you will even ever reach that but you are assured there won’t be clipping not even when (shortly) turning up the music to ‘irresponsibly’ and uncomfortable (for longer duration) listening levels.
When you simple don’t ever want to reach those levels but occasionally want to reach loud levels then the target should be 110dB SPL.
When the idea is to never play loud but only want to listen to ‘comfortable’ levels then 100dB SPL could be a target.
It sounds weird but even when one only listens to background music levels (60-70dB average) you will still need the system to be able to reach 90dB SPL in order to accurately reproduce any peaks and have some headroom left.
10dB is about a doubling of perceived loudness.

So now the ‘target max. SPL’ is known (can be chosen) and we need to know the sensitivity (in dBV).
One must make sure those numbers are correct. When only the efficiency number (in dB/mW) is known this needs to be converted to dB/V first.

All that is needed now is the table below, the dB/V number and what ‘max. peak SPL‘ you want to reach.
Subtract the headphone’s dB/V number from the max.peak SPL you want the headphone to reach.

As an example data for the 300Ω Sennheiser HD650 below:
This headphone is 103dB/V, we want to reach 110dB peaks so we find a difference of 7dB. The table above shows you need the amplifier to reach 2.2V.
Suppose using the same headphone (103dB/V) but we want to occasionally (and shortly listen to that great intro loud !) or with some EQ in the bass and not clip anything we want to be able to reach 120dB SPL then a 17dB difference is needed. Acc. to the table above we will need the amp to reach 7V

The data for the 48Ω Beyerdynamic DT 900 PRO X below:
This headphone is 117dB/V, we want to reach 120dB peaks so we find a difference of 3dB. The table above shows you need the amplifier to reach 1.4V.

And data for the 13Ω DCA ÆON closed below:
This headphone is 97dB/V, we want to reach 115dB peaks so we find a difference of 18dB. The table above shows you need the amplifier to reach 8V.

Once the required voltage is known and the impedance of the headphone is known we can determine how much ‘power‘ the amplifier/source needs to be able to reach.
For this the table below is required. The table shows for 6 ‘standard value’ impedance headphones how much power is drawn when the found voltage (from the previous step) in the left column is selected.
When a headphone is say .. 20Ω then the drawn/required power is between the value shown in the 16Ω and 32Ω box.

As an example data for the 300Ω Sennheiser HD650 below:
for 110dB peaks a voltage of 2.2V means about 0.012W (12mW) is required.
for 120dB peaks a voltage of 7V means about 0.16W (160mW) is required.
This means any amplifier that can reach > 160mW in 300Ω can effortlessly drive this headphone.
All that needs to be checked if the HD650 can handle this power… as the HD650 is rated 500mW this is no problem. 
Note: when an amplifier is only rated at say.. 200mW in 32Ω it can only reach about 2.5V and thus only reach 20mW in 300Ω (just check the table above).

And data for the 48Ω Beyerdynamic DT 900 PRO X below:
To reach 120dB peaks a voltage of 1.4V is needed. This is between 1 and 2V so best to use the 2V row.
The point where the 2V row intersects the 50Ω column the box states 0.08W (80mW).
The headphone is rated 30mW but … can handle 100mW peaks.
Now.. a problem is that in most cases output power is only listed at 32Ω and/or 300Ω and not at 50Ω.
50Ω still counts as a low impedance headphone (the tilt point is around 120Ω where we speak of high impedance).
We found 1.4V was required so look in the 2V row (for some extra headroom).
In the 32Ω column for the 2V row we find 130mW. This means that any headphone amp that is specified > 130mW in 32Ω can also drive the DT 900 PRO X as it will draw less than that.

The data for the 13Ω DCA ÆON closed below:
To reach 115dB peaks we need to reach 8V. The 8V row intersects with 16Ω column and we find no less than 4W but at 8V the lower impedance headphone will actually draw no less than 5W !
It thus requires an amplifier that can drive headphones with this low impedance. 
The solution here is (when the 115dB is a requirement) to connect it directly to the output of a speaker amplifier or find a headphone amp that can deliver at least 6W or so in 16Ω.

It is obvious not all headphones are equally sensitive and there can be huge differences between them.

home
back to articles
back to technical explanations