power, efficiency, levels, balanced, impedance

home
back to Learn

published: Dec-11-2013, last update: Oct-17-2022

Power levels, efficiency, impedance, voltages, current, balanced (bridged) versus single ended (common ground), sound pressure…
Can you make heads nor tails ?

read: headphone power and amplifiers and perhaps you can.
This article has in depth information about the power levels and how they relate to headphones and amplifiers.
It is rather technical but maybe things will become clearer even for technical illiterates

What is the relation between resistance and impedance and how will this affect the sound ?
In most forums there is lots of speculation, information and above all MIS-information about output resistances of amplifiers, impedances of headphones, cables and how they relate.
The biggest problem is there are facts and fiction mixed and spread over large quantities of posts. This makes it very difficult to discriminate between facts and nonsense.
The article resistance, impedance and other issues  covers a lot of often asked questions and puts them in an (I hope for most) understandable context.
It will let you catch up on some basics on resistance, impedance, damping factor, output resistance, cables.

Ever wondered HOW much power you actually need for your headphone(s) ?
Download the pdf from the link below:
https://www.mediafire.com/file/szz0cq3jkjzv2hr/headphone+power+table+2023.pdf/file
How much Voltage and/or Current and power is needed and.. how loud can your headphone actually play ?
The table has over 800 ‘familiar’ headphones in it (only on-ear and over-ear)

How loud you play your music will largely depend on our preference in music, recording quality (piercing treble,  lots of bass or a nice clean recording) and the dynamic range of that recording.To get an idea (it is not the final truth) about which album has how much dynamic range you can look for artists and albums HERE.
A high or low dynamic range doesn’t mean an album or song sounds better or worse. It only says something about how many dB’s peaks and average levels are apart. For instance an album with DR8 has peaks that are 8dB louder than the average levels.
The average level determines how loud we perceive the music and the peaks are not necessarily heard as peaks.
An album with a DR16 thus has 16dB higher peaks than the average levels and is more dynamic.

How loud do we actually play our music ?

This isn’t a really easy question to answer as it depends on how one prefers to listen and to what music.
More accurately how well a recording was made and what the Dynamic Range of the recording is.
Peaks can be much higher than the average levels and it is the average levels that more or less determine how loud one perceives the music.
A popular music recording with a DR6 or so you can’t turn up as far as a DR16 recording because the average levels are already 10dB louder. Out of interest in how loud I actually hear I decided to listen to a recording while measuring the output level of the amplifier.
The reason why you can’t really use a dB meter is because it averages, even in peak mode it doesn’t register very short attacks that well. At least the cheaper SPL meters I have. So I used a song from Paul Simon from the original CD.
The DR database had the following info:
Analyzed: Paul Simon / There Goes Rhymin’ Simon / 1987
DR13 -2.55 dB -19.57 dB 3:31 03-Take Me To The Mardi Gras
A DR13 recording is actually quite decent and this recording does sound very dynamic and free of distortion.

Test conditions:
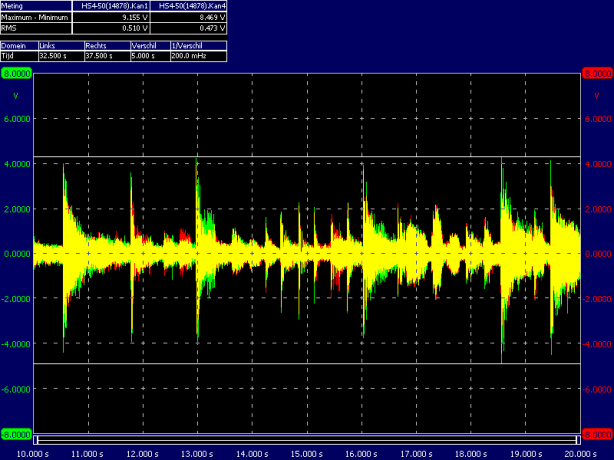
FiiO X3, line-out > Kameleon + HD650 module ↦ HD650 > my 55 y.o. ears.
the headphone signal was splitted to a HS4/50 oscilloscope in peak detect mode.
During a time frame of 10 seconds (in various parts of the song) the signal was logged and peaks were measured and displayed.
The RMS value of the 10 second section is shown as well as the peak-to-peak voltage.
As we want the RMS value of the peaks that occur we need to convert the peak-peak voltage to RMS.
To do this we need to find the peak value by halving the peak-peak value and take the √2.
As this factor will be the same for all calculations it is easier to multiply the peak-peak value with 0.354
Because we now have the RMS voltage and the impedance (320 Ω) we can calculate the power using ((U_RMS)² / 320)x1,000) = mW. The HD650 has an efficiency of 98dB @ 1mW (measured by Innerfidelity).
As the measured power and the amount of dB is known at 1mW we can calculate the SPL.

Below the scope data from a (random part in the song) chosen 10 second excerpt from the recording.

note: For young people (< 25.y.o.) the perceived loudness may be about 10dB lower than shown in the tests below.
The lower hearing limits climb upwards as one ages.
Young folks thus perceive sounds at the given power levels about 10dB louder (twice as loud) as older folks.

note2: dB SPL is not the same as dBA (or Phon). This article is about dB SPL and not dBA !

---

The part of the recording shown below was playing very softly, think soft level when listening in the evening. The level where you can easily listen for a whole evening while having the urge to turn up the volume a bit.
This is slightly below the level I usually listen at. My ‘normal’ listening level is around 75dB average.

This resulted in the following (rounded off) numbers:

RMS levels = 23mV = 0.0017mW = 70dB (average)
Peak levels = 245mV_PP = 87mV_RMS = 0.023mW = 82dB
calculated DR = 11.5dB for that 10 sec of the song.

---

The plot below shows part of the recording was playing at a very comfortable level that is a fair bit louder than the soft level. You can listen a whole evening to this level. This is slightly above the level I usually listen at.
On lower DR recordings you like to turn it down a slight nudge, higher DR recordings you may feel the urge to turn it up a tad.

This resulted in the following (rounded off) numbers:

RMS levels = 75mV = 0.018mW = 80dB (average)
Peak levels = 830mV_PP = 293mV_RMS = 0.26mW = 92dB
calculated DR = 11.8dB for that 10 sec of the song.

---

The  part of the recording below was playing at a comfortably loud level which is easy to listen to for 1 or 2 songs before getting the urge to turn it down to more comfortable levels.
When I really like a song I might turn up the volume to this level but turn it down again after 1 or 2 songs.

This resulted in the following (rounded off) numbers:

RMS levels = 236mV = 0.174 mW = 90dB (average)
Peak levels = 2.63V_PP = 930mV_RMS = 2.7mW = 102dB
calculated DR = 11.9dB for that 10 sec part of the song

---

This part of the recording below was playing uncomfortably loud. It is the type of level where you turn up the volume because you either like the song very much or want to listen ‘deep’ in the recording to evaluate.
Not a level you would gladly endure for the whole song.

This resulted in the following (rounded off) numbers:

RMS levels = 510mV = 0.81mW = 97dB (average)
Peak levels = 9.16V_PP = 3.24V_RMS = 33mW = 113dB
calculated DR = 16dB for that 10 sec part of the song
(this was the intro of the song by the way)

---

Here the music is playing at quite uncomfortably loud levels. One may use these levels for listening ‘in the recording’ for analytic purposes to check for distortions or find noise levels in the recording.
These levels are certainly NOT used for pleasantly enjoying music and one, for sure, cannot maintain to listen to these levels for the whole song.
It should be noted though that this is a DR13 recording and this particular part was ‘just’ 12dB DR.

When listening to DR20 recordings the average levels will be quite loud but the peak levels will reach about the same 117dB peak levels.
The amplifier started clipping the highest peaks already which added a sharp ‘edge’ at certain peaks.
I would not call those peaks anywhere near ‘pain levels’ though but ‘very loud’ none the less.

This resulted in the following (rounded off) numbers:
RMS levels = 1.35V = 5.6mW = 105dB (average)
Peak levels = 15V_PP = 5.3V_RMS = 88mW = 117dB peak
calculated DR = 11.9dB for that 10 sec part of the song.

I certainly do not recommend listening to these levels for longer than 1 minute or so.

---

This data shows that to drive the HD650’s to uncomfortable loud levels while still not nearing any clipping levels and having a few dB extra headroom you will need an amplifier that can supply at least 10V_RMS which means the amplifier must be able to supply 300mW into 300Ω headphones. When that amplifier is low resistance and can provide the same voltage in 32Ω headphones it must be specified for 3W into 32Ω.
To drive the HD650 to comfortably loud levels you only need around 1.7V_{RMS =} 10mW into 300Ω though.
A player that is specified to reach 100mW in 32Ω thus will be able to do that job.

Of course the voltage levels for driving an equally efficient (dB’s per mW) headphone will be substantially lower.
Currents will be the same magnitude higher.
The numbers above are thus only applicable to 250Ω to 300Ω headphones.
For the very few 600Ω headphones around you can multiply the needed VOLTAGES by a factor 2.

How much power do we need ?

Most headphones do not need a lot of power (check the efficiency table) play sufficiently loud.
Only very few inefficient ones do and these don’t even need that much power as most people think.

It doesn’t hurt to have a surplus of power available unless you are using headphones that cannot handle a lot of power.
In this case you run the risk of burning out the voice coils by accident (when not on the head) but will never run into clipping.
Having a surplus (in power) of a factor 10 won’t hurt but  may never or hardly ever be used.

Having too little power (voltage actually) won’t damage any voicecoils but higher impedance headphones won’t reach decent SPL levels.
Too little power results in not very dynamic and ‘meager’ sound in general.
Driving a high impedance headphone like HD800 or HD600 from a Sansa Clip won’t give a satisfying sound simply because the output voltage ‘clips’ before a decent listening level is reached. IF you only like to play music very softly there is no problem.
For this reason many people draw the conclusion they need more power .
They DO of course, as power is related to voltage but it is not that one needs more POWER.
P (watt) = U²(voltage) x impedance (Ohm), but what high impedance headphones really need is more voltage.

Because of these facts the myth is born ‘more power = better sound’.
It has some truth in it though.

Having an amp that can deliver 10W, if your headphone can only handle 0.2W, won’t sound better than when playing it from an amp that can deliver just 1W or maybe even ‘merely’ 0.1W (100mW).
Of course, you also need to include the psychological factor of having the ‘knowledge’ the amp will never reach its limits and you have ‘power’ in your hands.

For instance, an amp may deliver 1W into 16Ω but the same amp will only deliver 0.025W into a 600Ω headphone (assuming the current limit is not reached and output resistance is low)
Someone that THINKS he just bought a powerful amp (it is 1W for heavens sake!) will not be able to drive a 600Ω headphone very loud.
So one may think.. I need a much more powerful amp.
You don’t, you just need an amplifier with a higher output voltage, not necessarily meaning a more powerful amp.

It works the other way around too.
An amplifier that can deliver 1W into 600Ω only needs to deliver 40mA (60mA pk) to achieve that power.
Let’s assume the amp is current limited to 60mA.
When you connect a 20Ω headphone to that same amp it will only deliver 0.032W into it.

Power specs are thus MEANINGLESS unless they are accompanied by the headphone impedances that it must drive.
This too adds to the needs more ‘power’ or ‘headphone X or Y’ is hard to drive myths on the web.

This is just the technical part though, as many will say that doesn’t account for everything that is perceived.

Now, let’s assume we do not want to play very loud and have no need to play any louder than say 105dB peak levels.
This means for high DR recordings average levels of 90dB will be present

If you want to be able to drive all commercial headphones to 105dB (peak) but with NO headroom to spare, you will need an amplifier that can reach certain minimal voltage, current and thus power levels, remember P (Watt) = U (Volts) x I (Amps) .
We are going to differentiate between sensitive and ‘hard to drive’ headphones and 2 tranches in between those values.

Some examples of known headphones from the mentioned headphone power table

very sensitive low impedance headphone: (ATH-ES10 for instance) needs 0.25mW, 0.1V,  2.5mA to achieve 105dB SPL.
very sensitive high impedance headphone:  (GMP 435Sfor instance) needs 0.25mW, 0.25V,  1mA  to achieve 105dB SPL.

average sensitive low impedance headphone: (Beyer T70P) needs 1.26mW, 0.2V,  6mA
average sensitive high impedance headphone: (Beyer T70) needs 1.26mW, 0.6V,  2mA

average less sensitive low impedance headphone: (K550) needs 6mW, 0.5V, 13mA 
average less sensitive high impedance headphone: (DT770/600) needs 8mW,  2V,  4mA 

difficult ones like:
K172 needs 160mW, 3V, 50mA
K240 sextet (600 Ohm) needs 40mW, 4.9V, 8mA
one of the most demanding headphones around, the HE6 needs 630mW,  5.2V, 120mA
and the hardest exotic one K1000 needs 1.3W, 13V, 91mA

For 90dB average (105dB peak) on high DR recordings we need.
most sensitive headphones around: 0.2mW,  0.1V,  2mA  
average sensitive headphones: 1.6mW,  0.3V,  5.5mA
somewhat less sensitive headphones: 29mW, 1.7V,  17mA 
difficult to drive ones: 270mW, 4.5V, 60mA 
the VERY few insensitive ones: 1.5W, 13.5V, 110mA

For driving most common headphones to 105dB peak levels one ONLY needs 3V and 20mA  = 0.06W (60mW) which most simple and battery fed C’Moy amps should be able to deliver effortlessly.

When driving ONLY sensitive ones:
0.3V x 3mA = 0.1mW is needed that is 0.0001W which can be supplied by the smallest portable players/mobile phones.

Lets assume you want a beast of an amp or occasionally play at loud, but undistorted levels, and want to reach those peak levels of 120dB things change radically as currents and voltage levels increase by 15dB which means a factor 5.5 and for power even by a factor 30.

So IF you want to listen to an HE6  loud on high DR music:
HE-6:  15V x 360mA  = 5.5W

For average headphones  the amplifier needs to be able to deliver 6V and 50mA

For specific difficult ones like K172 = 1.6W, 10V, 165mA  or  K240 sextet (600 Ohm) 0.4W, 16V, 26mA

Lets assume you want a beast of an amp that has no problem playing peaks of 120dB things change radically as currents and voltage levels increase by a factor 5.5 and power by a factor 30

So IF you want to listen to an HE6 REALLY loud on high DR music:
HE-6:  29V x 0.6A  = 17W (voice coil would burn out !)

most sensitive headphones around: 6mW,  0.6V,  10mA 
average sensitive headphones: 50mW,  1.7V,  30mA 
somewhat less sensitive headphones: 1W, 9.5V,  100mA  (damage may occur to some)
difficult to drive ones: 8W, 24V, 0.33A   (some will never reach it and burn out !)
the VERY few insensitive ones: 45W, 75V, 0.6A  (those will never reach it and burn out !)

So IF you like to play high DR recordings really loud for very short periods you need high powered amps.
If you like to play high DR recordings comfortably loud, but with no headroom to spare you don’t need nearly that much.

Balanced versus single ended… what’s up with that ?

All amplifiers have a voltage limit and a current limit. voltage x current = power.
When one wants to double the voltage one can put those amplifiers in series.
This doubles the voltage but NOT the current.

When one wants to double the current one must put the amplifiers in parallel.
To illustrate look at the O2 schematic, it has op-amps in parallel to double the output current.
This, however, doesn’t double the voltage only the current.

When an amplifier is bridged (used balanced) there basically are 2 amplifiers in series.
This means double the voltage but not double the output current.

When one takes a look at output voltages of balanced and RCA output DAC’s as an example. The RCA out is 2V then the XLR is 4V.  As there is as good as no load at line level these voltages always double.

Now comes the output power part, there is a lot of confusion about this.

Lets assume the amplifier in question has unlimited current (for argument sake) and can put out max 10V in SE and 20V in balanced.

some calculations for impedances.

‘single ended’ = 10V and ‘balanced’ = 20V

8 Ohm = 12.5W(1.25A)  and 50W (2.5A)
16 Ohm = 6.25W(0.625A)  and 25W (1.25A)
32 Ohm = 3.125W(0.313)  and 12.5W (0.625A)
64 Ohm = 1.56W(0.156A)  and 6.25W (0.313A)
128 Ohm =  0.78W(0.078A)  and 3.125W (0.156A)
256 Ohm = 0.39W(0.039A)  and 1.56W (0.078A)
512 Ohm = 0.19W (0.019A) and 0.78W(0.039A)

It is evident the output voltage is doubled and as a result of power = voltage x current (and current being voltage divided by resistance) is (voltage x voltage)/resistance. This means power is 4x higher in balanced mode.
What is also clear is that lower impedances require a lot more current than higher impedances

Now comes the more difficult part in this story.  The amplifiers are current limited. This means each amplifier can deliver 10V max and 250mA (0.25A).
In balanced mode these are in series so the output voltage can be double (and power quadrupled) as long as the current limit is not reached.

The amplifiers are in series so max. current remains the same in SE and balanced mode. Power = (current x current) x resistance.

same table but now current limited at 250mA = 0.25A (with infinite output voltage): ‘single ended’ and ‘balanced’
8 Ohm = 0.5W(2V)  and 0.5W (2V)
16 Ohm = 1W(4V)  and 1W (4V)
32 Ohm = 2W(8V)  and 2W (8V)
64 Ohm = 4W(16V)  and 4W (16V)
128 Ohm =  8W(32V)  and 8W (32V)
256 Ohm = 16W(64V)  and 16W (64V)
512 Ohm = 32W (128V) and 32W(128V)

As can be seen high voltages are needed when high power levels are needed in high impedances.

Now to figure out how much power there is when the amp is voltage and current limited all we have to do is look for the highest voltage the amp can put out (10V in single ended and 20V in balanced) in the above current table.

So for single ended (max 10V) and balanced (max 20V) we can see at certain impedances ,and 250mA current limit, voltages above 10V and 20V respectively are required but are not available.

8 Ohm = 0.5W(2V)  and 0.5W (2V)
16 Ohm = 1W(4V)  and 1W (4V)
32 Ohm = 2W(8V)  and 2W (8V)
64 Ohm = 4W(16V)  and 4W (16V)
128 Ohm =  8W(32V)  and 8W (32V)
256 Ohm = 16W(64V)  and 16W (64V)
512 Ohm = 32W (128V) and 32W(128V)

For voltages we can look in the table below that belong to the impedances and max currents (thus power). Here too there is a limit which in this case is 250mA both for single ended as well as balanced. Every level above 250mA (0.25A) thus is not possible.
This means we can strike out power levels requiring currents above 0.25A.

8 Ohm = 12.5W(1.25A)  and 50W (2.5A)
16 Ohm = 6.25W(0.625A)  and 25W (1.25A)
32 Ohm = 3.125W(0.313)  and 12.5W (0.625A)
64 Ohm = 1.56W(0.156A)  and 6.25W (0.313A)
128 Ohm =  0.78W(0.078A)  and 3.125W (0.156A)
256 Ohm = 0.39W(0.039A)  and 1.56W (0.078A)
512 Ohm = 0.19W (0.019A) and 0.78W(0.039A)

Now due to the impedances being stepped in factors of 2 the power levels that can be reached differ a bit in current and voltage.

Below the ‘borders’ once more.

32 Ohm = 2W(8V)  and 2W (8V)  versus 3.125W(0.313A)  and 12.5W (0.625A)
64 Ohm = 4W(16V)  and 4W (16V) versus 1.56W(0.156A)  and 6.25W (0.313A)
128 Ohm =  8W(32V)  and 8W (32V) versus 0.78W(0.078A)  and 3.125W (0.156A)

So the limits are somewhere between these values because there is current and voltage limiting in these amps.

For low impedance headphones the power is limited by current (which is the same for both amps so below a certain impedance the max. power is the same as shown in the current table BUT the voltages associated with that voltage can not be reached.

For high impedance the max power is determined by the output voltage so above a certain impedance the output voltage can be up to 2x higher in the balanced (20V) version.

8 Ohm = 0.5W(2V)  and 0.5W (2V)  = current limited
16 Ohm =  0.5W(2V)  and 0.5W (2V) = current limited
32 Ohm =  2W(8V)  and 2W (8V) = current limited
64 Ohm = 1.56W(10V) = voltage limited and 4W (16V) = current limited
128 Ohm =  0.78W(10V)  and 3.125W (20V)  = voltage limited
256 Ohm = 0.39W(10V)  and 1.56W (20V)  = voltage limited
512 Ohm = 0.19W (10V) and 0.78W(20V)  = voltage limited

As can be seen above a certain impedance the power quadruples and below a certain impedance the power is actually the same with a small transition between same power and quadruple power between 32 Ohm and 128 Ohm and peaking somewhere around 64 Ohm in this case.

At 10V and 250mA one can calculate the maximum power as being 2.5W for which one needs 40 Ohm.
At 20V and 250mA the max power is 5W for which one needs 80 Ohm.

Efficiency / sensitivity….
not as straightforward as one might think.

Ever wondered why a headphone with an efficiency of 105dB could still play louder than another headphone with an efficiency of 112dB ?
….. The short answer is that one headphone is specified in dB/mW and the other one is specified in dB/V. These specifications are VERY different as dB/mW is specified at 1mW and the dB/V is specified at 1V.
1V is NOT the same as 1mW.

Ever wondered why a headphone with a efficiency of 98dB/mW can play louder (or softer) than another headphone that is also specified at 98dB/mW ?
….. The short answer is that when headphones with equal dB/mW efficiency numbers BUT different impedances are connected to the same voltage (an amplifier is a voltage source) they will not be dissipating the same amount of power and thus will not sound equally loud.

Ever wondered how headphone-A can still sound louder than headphone-B on certain amplifiers yet not on others while both headphones are specified with the same efficiency of 110dB/V ?
….. While two headphones with the same efficiency number in dB/V BUT with a different impedance will sound equally loud on a low output resistance amplifier, they will differ several dB’s in SPL when connected to an amplifier with a higher output resistance.

The key in all these cases is a MIX of headphone impedance, output resistance of the amplifier, Watts and Volts.
This makes it impossible, or at least very hard, to compare efficiency numbers (directly).

For those who want to know a bit more about ins and outs as well as the math behind it you may want to read further because below there is more detailed info about this subject.

The efficiency number in the specs of a headphone tells you something about how loud a headphone will play when a certain amount of power or voltage is applied.
The dBm number (often noted as dB/mW) tells us how much dB SPL (Sound Pressure Level) is generated when 1mW of power is applied.

The dBV (often noted as dB/V) number tells us how much dB SPL is generated when 1 Volt is applied.
For this reason both efficiency numbers are listed side-by-side in the headphone power table.

Some manufactures specify the efficiency numbers in dBm, others in dBV, some do not specify it at all or just produce a number and forget to even add the ‘m(W)’ or ‘V’ behind the dB value.
This makes the specified numbers quite confusing as dBm and dBV numbers differ substantially and can NOT be compared directly and need to be converted to the other spec.

From a technical point of view, where we want to use the numbers to compare how loud a headphone plays compared to another one, provided we do NOT touch the volume control, the dBV number is the best tool for direct comparisons.
The reason for that is that amplifiers provide a Voltage and not power.
This is only true when the output resistance of the amplifier is very low (a few Ohm max) though.

The dBm number cannot as easily be used to compare how loud a headphone will play compared to another one that is also specified in dBm.
The reason for this is the fact that an amplifier doesn’t supply the same amount of mW (milli Watt = 0.001W) into different impedance headphones when the volume control is in the same position.
Reason being the amplifier delivers a voltage.

A few examples and calculations may illustrate this better.

Let’s assume an amplifier puts out 1V.
When the output resistance is close to 0Ω (Ohm) this means that the 1V will be there regardless of the load impedance.
A 32Ω headphone thus will have 1V on it AND a 600Ω headphone will also have 1V on it.
This changes when the amplifier has a higher output resistance because of voltage division, this is discussed below.

For now we will use the 0Ω amplifier in this example.

When a 32Ω headphone is specified as 120dBV it will produce 120dB SPL when 1V is applied.
When a 600Ω headphone is specified as being 100dBV, this means when 1V is applied it produces 100dB SPL.
A dB scale is not linear, Volts is.
A headphone with a 120dBV specification for example therefore won’t produce 121dB SPL when the applied voltage is doubled, nor will it produce 240dB SPL in that case.
A 6dB increase in SPL is a doubling of the voltage, a 6dB decrease in SPL means a halving of the applied voltage.
A 10dB increase in SPL is perceived as a doubling in SPL(volume) while a decrease in 10dB is perceived as almost a halving in SPL.

The handy part of this dBV specification is that one can directly see the relation between the loudness of the 2 headphones.
In this example the 32Ω headphone = 120dBV and the 600Ω version = 100dBV.
In these specs you can immediately see that when the same voltage is applied (1V) the 32Ω headphone plays 20dB louder than the 600Ω version.
Since 10dB is a doubling of perceived loudness the 32Ω headphone will play roughly 4x louder.

For dBm specified headphones this is NOT the case, the numbers can NOT be compared directly.
The reason for this is that an amplifier delivers an output voltage and not an amount of power (mW).
There is a relation of course.
A 3dB increase in SPL is a doubling of power, a 3dB decrease in SPL is a halving of applied power.
The observant reader may have noticed that doubling the power only increases the SPL by 3dB, yet doubling the voltage increases the SPL by 6dB.
This is no coincidence as the following formula is applicable P=U2/R.
P = Power and is expressed in Watt
U = Voltage expressed in Volt
R = Resistance expressed in Ohm
Note: because headphone power is expressed in mW(att) instead of Watt the outcome of the formula must be multiplied by 1000.

As one can see Power has a relation to voltage (U) AND resistance as R is also present in the formula P=U2/R.
Note: A headphone has an impedance which basically is a resistance that varies depending on the frequency. An impedance is usually indicated by the letter Z instead of R but the formula remains the same. More accurately for most headphones the formula would be P=U2/Z.
However, the efficiency of most headphones is measured around 1kHz.
At this frequency the impedance of most headphones behaves very linear, as if it was a resistance so for efficiency measurements it doesn’t matter that much.

Because the amount of mW has a relation with the impedance the dBm numbers cannot be compared between headphones with different impedances.
They CAN be compared between headphones with the SAME impedance though.

As an example we have 2 headphones with an efficiency of 100dBm.
One headphone is 32Ω and the other one 120Ω.
BOTH headphones thus will produce 100dB SPL when 1mW of power is applied.
But… amplifiers (low output resistance ones) put out voltage and not power.
For this reason the 32Ω headphone (with a 100dBm efficiency) will sound louder than the 120Ω headphone (also with a 100dBm efficiency) when the volume control is left unchanged.
The reason is because a voltage is applied.
To compare these headphones the dBm values have to be converted to dBV.

Now some math….

P=U²/R so U²=PxR and if we want to know the voltage: SQRT(U=(PxR)).
Because the dBm number is always specified at 1mW the P can be substituted by 0.001
SQRT (U=(0.001xR)) where R is the impedance (in Ω) of the headphone and U is the applied voltage (in Volt).

For a 32Ω headphone: SQRT (U=(0.001×32)) = 0.179V
For a 120Ω headphone: SQRT (U=(0.001×120)) = 0.346V

So… to get 100dB SPL both headphones need 1mW BUT the 32Ω headphone needs only 0.179V and the 120Ω needs 0.346V to reach that 1mW.
While the efficiency numbers are the same, the lower impedance headphones needs less voltage to reach the same 100dB SPL.

Because an amplifier provides a voltage, the lower impedance headphone will thus sound louder than the higher impedance one, as with the same voltage applied the dissipated power is higher.

To convert the dBm to dBV we need to calculate the factor between 1V (the reference in the dBV spec) and the calculated value from the dBm calculation (0.179V for 32Ω and 0.346V for 120Ω).
32Ω headphone: 1V/0.179V = factor 5.58
120Ω headphone: 1V/0.346 = factor 2.89
As efficiency is specified in dB we need to calculate the amount of dB the calculated factor represents.
The formula for voltage to dB conversion = 20xLOG(factor).
32Ω headphone: factor 5.58 = +14.9dB louder than 100dB = 114.9dBV
120Ω headphone: factor 2.89 = +9.2dB louder than 100dB = 109.2dBV

After the conversion we can clearly see the 32Ω headphone produces a 5.7dB higher SPL than the 120Ω headphone.

Let’s do some more math but reason in the other direction…

We will apply 1V to both these headphones (32Ω and 120Ω with a 100dBm efficiency) and will calculate the dissipated power with the formula P=U²/R.
32Ω headphone: (1)2 / 32 = 0.0313W = 31.3mW
120Ω headphone: (1)2 / 120 = 0.0083 = 8.3mW
It is evident that the lower impedance headphone dissipates more power than the higher impedance one. As it receives more power it will also play louder.
The 32Ω headphone has 3.77x more power than the 120Ω headphone.
To convert the difference in power to dB we can use the formula: 10xLOG(factor)
10xLOG(3.77) = +5.7dB

While is is clear that two headphones with the same efficiency in dBV will play equally loud on amplifier-X can still differ in SPL when connected to amplifier-Y.
The reason for this is amplifier-X and Y have a different output resistance in this case AND the headphones also have a different impedance. This is caused by voltage division.
The output resistance of an amplifier is in series with that of the connected headphone.
The voltage across the output resistor and the headphone impedance will divide in the same ratio.
When the output voltage across headphone-A is adjusted so it is 1V the voltage BEFORE the output resistor will therefore be higher depending on ratio between these two resistances.
Again some math to show why.

Headphone-A has 110dBV efficiency and a 32Ω impedance.
Headphone-B has 110dBV efficiency and a 50Ω impedance.
Amplifier-X has 0.1Ω output resistance.
Amplifier-Y has 32Ω output resistance.
Amplifier-Z has 120Ω output resistance.

The amplifiers are all adjusted to produce 1V with headphone-A connected.
For amplifier-X the ratio between headphone-A and the output resistance is 32:0.1 = 1:320.
When we adjusted the voltage across headphone-A to be 1V it will produce 110dB SPL.
Because these resistances are in series there is 1/320^thof 1V present across the output resistor (3.1mV).
Before the output resistor there is thus 1.0031V present (1V across the headphone + 0.0031V across the output resistor)
When we do not touch the volume control that 1.0031V will remain there regardless of the load (assuming enough current is available).
Now we change headphone-A to headphone-B.
The ratio also changes to 50:0.1 (500:1) and thus the voltage division changes.
There will still be 1.0031V on the voltage divider so (50/(50+0.1)) x 1.0031V = 1.001V.
It is clear that there isn’t much difference between 1V and 1.001V and when we calculate the difference in dB the difference this is only (around) 0.01dB.
This means headphone-A will produce 110dB and headphone-B will produce 110.01dB when connected to amplifier-X
To discern a difference this has to be at least 0.5dB and 0.01dB is MUCH smaller than that.

When the same procedure is repeated with amplifier-Y (32Ω output resistance) things already change.
The ration is now 32:32 = (1:1)
Again we adjust the voltage across the headphone to 1V exactly.
The voltage BEFORE the output resistor is thus now set to 2V instead of 1.0031 in the case of amp-X.
Now we change headphone-A to headphone-B again and thus the ratio changes from 32:32 to 50:32 (1.56:1).
There will now be 2V over the divider.
The voltage across the 50Ω headphone can thus be calculated as (50/(50+32)) x 2V = 1.22V.
The 50Ω headphone has a factor 1.22x higher voltage across it.
When we convert this difference to dB we find a value of +1.7dB.
|This means that when headphone-A is connected to amplifier-Y it will produce 110dB SPL but headphone-B ,connected to the same amp-Y will produce 111.7dB SPL.
That 1.7dB difference is audible (not obviously so, just slightly louder).

Lets repeat the same procedure with amplifier-Z which has a 120Ω output Resistance.
Ratio headphone-A and amp-Z is 32:120 = 1:3.75
When the output of amp-Z is adjusted to 1V on headphone-A the voltage BEFORE the output resistance will be 4.75V (3.75V across the output resistor and 1V across the headphone)
When the headphone is changed from A to B the ratio changes from 1:3.75 to 1:2.4 (50:120)
There will now be 4.75V across the voltage divider so the voltage across the 50 Ohm headphone can be calculated as (50/(50+120)) x 4.75V = 1.4V.
When we convert the difference between 1V and 1.4V to dB we find a difference of 2.9dB.
This means that when headphone-A is connected to amplifier-Z it will produce 110dB SPL but when headphone-B is connected to the same amp will produce 112.9dB SPL, 2.9dB is audibly louder.

The lesson we learned today is… be careful when looking at efficiency numbers and beware of the notation and impedances given in the specs before comparing the efficiency numbers with those of other headphones.

Can headphones be connected directly to speaker output  terminals ?
What about headphone power and speaker power how are they related ?
Do you need a resistor divider network and how to calculate and make them ?
The answers for this are found ON THIS PAGE

home
back to Learn